Hex, Bugs and More Physics | Emre S. Tasci

Clustering (or grouping) items using a defined similarity of selected properties is an effective way to classify the data, but also (and probably more important) aspect of clustering is to pick up abnormal pieces that are different from the other clusterable "herd". These exceptions may be the ones that we’re looking (or unlooking) for!

There is this simple clustering method called K-means Clustering. Suppose that you have N particles (atoms/people/books/shapes) defined by 3 properties (coordinates/{height, weight, eye color}/{title,number of sold copies,price}/{number of sides,color,size}). You want to classify them into K groups. A way of doing this involves the K-means Clustering algorithm. I have listed some examples to various items & their properties, but from now on, for clarity and easy visionalizing, I will stick to the first one (atoms with 3 coordinates, and while we’re at it, let’s take the coordinates as Cartesian coordinates).

The algorithm is simple: You introduce K means into the midst of the N items. Then apply the distance criteria for each means upon the data and relate the item to the nearest mean to it. Store this relations between the means and the items using a responsibility list (array, vector) for each means of size (dimension) N (number of items).

Let’s define some notation at this point:

• Designate the position of the k^th mean by m_k.
• Designate the position of the j^th item by x_j.
• Designate the responsibility list of the k^th mean by r_k such that the responsibility between that k^th mean and the j^th item is stored in the j^th element of r_k. If  r_k[j] is equal to 1, then it means that this mean is the closest mean to the item and 0 means that, some other mean is closer to this item so, it is not included in this mean’s responsibility.

The algorithm can be built in 3 steps:

0. Ä°nitialize the means. (Randomly or well calculated)

1. Analyze: Check the distances between the means and the items. Assign the items to their nearest mean’s responsibility list.

2. Move: Move the means to the center of mass of the items each is responsible for. (If a mean has no item it is responsible for, then just leave it where it is.)

3. Check: If one or more mean’s position has changed, then go to 1, if not exit.

That’s all about it. I have written a C++ code for this algorithm. It employs an object called kmean (can you guess what it is for? ) which has the properties and methods as:

class kmean
{
 private:
  unsigned int id,n;//"id" is for the unique identifier and "n" is the total number of items in the world.
  double x,y,z;//coordinates of the mean
  gsl_vector * r;//responsibility list of the mean
  char buffer [150];//some dummy variable to use in the "whereis" method
  unsigned int r_tott;//total number of data points this mean is responsible for

 public:
  kmean(int ID,double X, double Y, double Z,unsigned int N);
  ~kmean();
  //kmean self(void);
  int move(double X, double Y, double Z);//moves the mean to the point(X,Y,Z)
  int calculate_distances(gsl_matrix *MatrixIN, int N, gsl_matrix *distances);//calculates the distances of the "N" items with their positions defined in "MatrixIN" and writes these values to the "distances" matrix
  char * whereis(void);//returns the position of the mean in a formatted string
  double XX(void) {return x;}//returns the x-component of the mean’s position
  double YY(void) {return y;}//returns the y-component of the mean’s position
  double ZZ(void) {return z;}//returns the z-component of the mean’s position
  int II(void) {return id;}//returns the mean’s id
  int NN(void) {return n;}//returns the number of items in the world (as the mean knows it)
  int RR(void);//prints out the responsibility list (used for debugging purposes actually)
  gsl_vector * RRV(void) {return r;}//returns the responsibility list
  int set_r(int index, bool included);//sets the "index"th element of the responsibility list as the bool "included". (ie, registers the "index". item as whether it belongs or not belongs to the mean)
  int moveCoM(gsl_matrix *MatrixIN);//moves the mean to the center of mass of the items it is responsible for
  int RTOT(void) {return r_tott;}//returns the total number of items the mean is responsible for
  };
int check_distances(gsl_matrix* distances, int numberOfWorldElements, kmean **means);//checks the "distances" matrix elements for the means in the "means" array and registers each item in the responsibility list of the nearest mean.
double distance(double a1, double a2,double a3,double b1,double b2,double b3);//distance criteria is defined with this function

Now that we have the essential kmean object, the rest of the code is actually just details. Additionaly, I’ve included a random world generator (and by world, I mean N items and their 3 coordinates, don’t be misled). So essentialy, in the main code, we have the following lines for the analyze section:

  for (i=0;i<dK;i++)
   means[i]->calculate_distances(m,dN,distances);
  
  check_distances(distances,dN,means);

which first calculates the distances between each mean (defined as elements of the means[] array) and item (defined as the rows of the m matrice with dNx4 dimension (1st col: id, cols 2,3,4: coordinates) and writes the distances into the distances matrice (of dimensions dNxdK) via the calculate_distances(…) method. dN is the total number of items and dK is the total number of means. Then analyzes the distances matrice, finds the minimum of each row (because rows represent the items and columns represent the means) and registers the item as 1 in the nearest means’s responsibility list, and as 0 in the other means’ lists via the check_distances(…) method.

Then, the code executes its move section:

  for(i=0; i<dK; i++)
  {
   means[i]->moveCoM(m);
   […]
  }

which simply moves the means to the center of mass of the items they’re responsible for. This section is followed by the checkSufficiency section which simply decides if we should go for one more iteration or just call it quits.

  counter++;
  if(counter>=dMaxCounter) {f_maxed = true;goto finalize;}

  gsl_matrix_sub(prevMeanPositions,currMeanPositions);
  if(gsl_matrix_isnull(prevMeanPositions)) goto finalize;
  […]
  goto analyze;

as you can see, it checks for two things: whether a predefined iteration limit has been reached or, if at least one (two 😉 of the means moved in the last iteration. finalize is the section where some tidying up is processed (freeing up the memory, closing of the open files, etc…)

The code uses two external libraries: the Gnu Scientific Library (GSL) and the Templatized C++ Command Line Parser Library (TCLAP). While GSL is essential for the matrix operations and the structs I have intensely used, TCLAP is used for a practical and efficient solution considering the argument parsing. If you have enough reasons for reading this blog and this entry up to this line and (a tiny probability but, anyway) have not heard about GSL before, you MUST check it out. For TCLAP, I can say that, it has become a habit for me since it is very easy to use. About what it does, it enables you to enable the external variables that may be defined in the command execution even if you know nothing about argument parsing. I strictly recommend it (and thank to Michael E. Smoot again 8).

The program can be invoked with the following arguments:

D:\source\cpp\Kmeans>kmeans –help

USAGE:

   kmeans  -n <int> -k <int> [-s <unsigned long int>] [-o <output file>]
           [-m <int>] [-q] [–] [–version] [-h]

Where:

   -n <int>,  –numberofelements <int>
     (required)  total number of elements (required)

   -k <int>,  –numberofmeans <int>
     (required)  total number of means (required)

   -s <unsigned long int>,  –seed <unsigned long int>
     seed for random number generator (default: timer)

   -o <output file>,  –output <output file>
     output file basename (default: "temp")

   -m <int>,  –maxcounter <int>
     maximum number of steps allowed (default: 30)

   -q,  –quiet
     no output to screen is generated

   –,  –ignore_rest
     Ignores the rest of the labeled arguments following this flag.

   –version
     Displays version information and exits.

   -h,  –help
     Displays usage information and exits.

   K-Means by Emre S. Tasci, <…@tudelft.nl> 2007

 The code outputs various files:

<project-name>.means.txt : Coordinates of the means evolution in the iterations
<project-name>.meansfinal.txt : Final coordinates of the means
<project-name>.report : A summary of the process
<project-name>.world.dat : The "world" matrice in Mathematica Write format
<project-name>.world.txt : Coordinates of the items (ie, the "world" matrice in XYZ format)
<project-name>-mean-#-resp.txt : Coordinates of the items belonging to the #. mean

and one last remark to those who are not that much accustomed to coding in C++: Do not forget to include the "include" directories! 

Check the following command and modify it according to your directory locations (I do it in the Windows-way 🙂

g++ -o kmeans.exe kmeans.cpp -I c:\GnuWin32\include  -L c:\GnuWin32\lib -lgsl -lgslcblas -lm

(If you are not keen on modifying the code and your operating system is Windows, you also have the option to download the compiled binary from here)

The source files can be obtained from here.

And, the output of an example with 4000 items and 20 means can be obtained here, while the output of a tinier example with 100 items and 2 means can be obtained here.

I’m planning to continue with the soft version of the K-Means algorithm for the next time…

References: Information Theory, Inference, and Learning Algorithms by David MacKay

The (7,4) Hamming Code is a system that is used for sending bits of block length 4 (16 symbols) with redundancy resulting in transmission of blocks of 7 bits length. The first 4 bits of the transmitted information contains the original source bits and the last three contains the parity-check bits for {1,2,3}, {2,3,4} and {1,3,4} bits.

It has a transmission rate of 4/7 ~ 0.57 . Designate the source block as s, the transmission operator as G so that transmitted block t is t = G^Ts and parity check operator is designated as H where:

 This could be more obvious if we investigate the G^T and keeping in mind that, the first 4 "transformed" bits stay the same with 3 added to the end for parity check. So our parity reporter operator P would be:

As it calculates the parities for bits, also its Modulo wrt 2 must be included. Since we’re calculating the parities for {1,2,3}, {2,3,4} and {1,3,4} bit-groups, the values of the P are easily understandable. Now, we will join the Identity Matrix of order 4 (for directly copying the first 4 values) with the P operator to construct the G^T transformation (encoder) operator:

and H is actually nothing but [-P I₃]. It can be seen that HG^Ts will always result {0,0,0} in a parity check, meaning that all three parities have passed the test. So, where is the problem?

Noise: Noise is the operator that flips the values of bits randomly with an occuring probability f. Suppose that we have a source signal block of 4 bits length: {s₁, s₂, s₃, s₄}. I encode this information with calculating the parities and adding them to the end, thus coming up with a block of 7 bits length and call this block as t (for transmitted):

t=G^Ts (supposing t and s are given as column vectors. Otherwise, t=sG)

Now I send this packet but on the road to the receiver, the noise changes it and so, the received message, r, is the transmitted message (t) AND the noise (n):

r=t+s

Since I have got the parity information part (which may also have been affected by the noise), I compare the received data’s first 4 values with the parity information stored in the last 3 values. A very practical way of doing this is using 3 intersecting circles and placing them as:

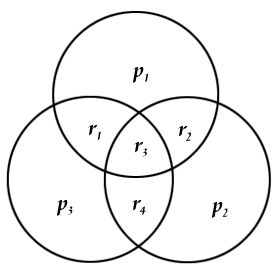
with r₁-r₄ representing the first values (ie, actual data) received and p₁-p₃ being the parity information (the last 3 values). So we place the values to their corresponding locations and easily can check if the parity matches to the related values. We can have 8 different situations at this moment. Let’s denote the z=Hr vector as the parity check result. z={0,0,0} if all three parity information agrees with the calculated ones, z={1,0,0} if only p₁ is different from the calculated parity of {r₁,r₂,r₃}, z={1,0,1} if p₁ AND p₃ are different from their corresponding calculated parities and so on. If there is only 1 error (ie, only one "1" and two "0") in the parity check, then it means that, the noise affected only the parity information, not the data encoded (ie, the first 4 values), so the corrupted data can be fixed by simply switching the faulty parity. If there are 2 parity check errors, this time, the value on the intersection of the corresponding parities (ie, r₁ for p₁&p₃, r₂ for p₁&p₂ and r₄ for p₂&p₃,) must be switched. If z={1,1,1} then r₃ should be switched.

Let’s introduce some mathematica operations and then tackle with some examples. You can just copy and paste them since there are no additional libraries required:

mGT = {{1,0,0,0},{0,1,0,0},{0,0,1,0},{0,0,0,1},{1,1,1,0},{0,1,1,1},{1,0,1,1}};
mH = {{1,1,1,0,1,0,0},{0,1,1,1,0,1,0},{1,0,1,1,0,0,1}};

(mS = {{1},{1},{1},{0}});
Mod[(mGTS=mGT . mS),2] // MatrixForm
mN ={0,0,0,0,0,0,1};
(mR = Mod[mGTS+mN,2])  // MatrixForm
mZ = Mod[mH . mR,2];
Flatten[mZ]

The first two lines define G^T and H and from here, you can check a very important property being:

 Mod[mH.mGT,2] // MatrixForm

 equal to 0.

We introduce the 4bit data to be transmitted as mS which we had referred as s through out the text. Then we encode the data to be send with the parity info encoded as mGTS (t) add a noise mN (n) to it assuming it is corrupted in the transmission process and the data the other side receives is mR (r) consisting of the data transmitted AND the noise acted on it. mZ is the parity check result (z) (I’ve "Flatten"ed it for a better view). In the operations above, the "Mod" operator is frequently used because of our universe being a mod2 universe (2=0, 3=1, 4=0,… just 0s and 1s actually!).

So, in this example, we had s={1,1,1,0}, and this was encoded as t={1,1,1,0,1,0,0} and on its way to the happy-ending, a noise corrupted it and switched its 3rd parity information from 0 to 1. As a result of this, the recipient got its data as r={1,1,1,0,1,0,1}. But since our recipient is not that dull, a parity check is immediately applied and it was seen that z={0,0,1} meaning that, there is something wrong with the 3rd parity information, and nothing wrong with the information received at all!

Now, let’s apply all the possible noises given that only one value can be switched at a time (ie, only one 1 in the n vector with the remaining all being 0s).

 For[i = 1, i <= 7, i++,
    mN = {0, 0, 0, 0, 0, 0, 0} ;
    mN = ReplacePart[mN, 1, i];
    mR = Mod[mGTS + mN, 2];
    mZ = Mod[mH . mR, 2];
    Print[mN, "\t", Flatten[mZ]];
    ];

After this, if everything went right, you’ll see the output something like this:

{1,0,0,0,0,0,0}   {1,0,1}
{0,1,0,0,0,0,0}   {1,1,0}
{0,0,1,0,0,0,0}   {1,1,1}
{0,0,0,1,0,0,0}   {0,1,1}
{0,0,0,0,1,0,0}   {1,0,0}
{0,0,0,0,0,1,0}   {0,1,0}
{0,0,0,0,0,0,1}   {0,0,1}

So we know exactly what went wrong at are able to correct it… Everything seems so perfect, so there must be a catch…

There is no decoding error as long as there is only 1 corruption per data block!

As the corruption number increases, there is no way of achieving the original data send with precise accuracy. Suppose that we re-send our previous signal s={1,1,1,0} which yields t={1,1,1,0,1,0,0} but this time the noise associated with the signal is n={0,1,0,0,0,0,1} so, the received signal is r={1,0,1,0,1,0,1}. When we apply the partition check, we have z={1,1,1}, which means that, there is a problem with the 3rd value and we deduce that the original message transmitted was t={1,0,0,0,1,0,1} which passes the parity check tests with success alas a wrongly decoded signal!

The probability of block error, p_B is the probability that there will at least be one decoded bit that will not match the transmitted bit. A little attention must be paid about this statement. It emphasizes the decoded bit part, not the received bit. So, in our case of (4,7) Hamming Code, there won’t be a block error as long as there is only one corrupted bit in the received bit because we are able to construct the transmitted bits with certainty in that case. Only if we have two or more bits corrupted, we won’t be able to revive the original signal, so, p_B scales as O(f²).

References : I have heavily benefitted from David MacKay’s resourceful book Information Theory, Inference, and Learning Algorithms which is available for free for viewing on screen.

Information Theory, Inference, and Learning Algorithms by David MacKay

Mathematica Library for DataMining
Functions Library Intended To Be Used In DataMining Procedures
11/2007
Emre S. Tasci
S&C / MSE / 3mE / TUDelftFunctions List (EF: Required External Functions)

• Int DMBooleEST[statement_]
  Converts True/False => 1/0
  EF – NONE
• Bool DMBooleEST[statement_]
  Converts 1/0 => True/False
  EF – NONE
• Int DMCondEntropyEST[MatrixIN_,var2_,var1_, posVal1_, posVal2_,probVar1_]
  Calculates the Conditional Entropy H(var2|var1)
  EF – MSelectEST, DMProbeEST, DMEntropyEST
• Int DMEntropyEST[problist_]
  Calculates the entropy given the probability list “problist”
  EF – NONE
• Matrix DMGenMatrixEST[dim_,file_]
  Generates a Matrix of [dim,dim] dimension and writes this matrix to the “file” file. Returns the matrix generated.
  EF – DMBooleEST, DMUnitizeEST
• List DMInfGainEST[MatrixIN_,varno_]
  Calculates the Information Gain related to the “varno” variable wrt to the remaining variables.
  EF -Â MDiffElementEST , MSwapEST, DMCondEntropyEST, DMEntropyEST, DMProbeEST
• Vector DMProbeEST[MatrixIN_,varno_,varlist_]
  Calculates the probabilities of the variables’ possible outcomes.
  EF – NONE;

Important!!! ————————————

Assumed form of the MatrixIN: ;



(i.e., values for the same variable are stored in ROWS, NOTÂ in COLUMNS!)

Mathematica Library for additional Matrix Functions

Functions Library Intended To Be Used In Matrix Procedures 11/2007 Emre S. Tasci S&C / MSE / 3mE / TUDelft Functions List (EF: Required External Functions)

• List MDiffElementEST[matrixIN_,varno_]
  Returns the list of the different elements in the (varno). row of the specified matrixIN 
  EF – NONE
• List MPolluteEST[mx_,row_,ratio_]
  Assigns a 0 or 1 (with equal probabilities) to the randomly selected "ratio" of the elements of the matrix "mx" and returns the new "polluted" matrix.If "mx" is a List, then "row" is not relevant.
  *EF – NONE;
• List MSelectEST[MatrixIN_,varno1_,varval1_, varno2_] 
  Returns the list of "varno2" variables from the "MatrixIN" where "varno1" values equal to "varval1" 
  EF – NONE / AppendRows from LinearAlgebra`MatrixManipulation` (Optional)
• List MSwapEST[MatrixIN_,row1_,row2_] 
  Swaps the rows "row1" and "row2" in matrix "MatrixIN" 
  EF – NONE

Important!!!

Assumed form of the MatrixIN: ; (i.e., values for the same variable are stored in ROWS, NOT in COLUMNS!)

Renderu – LaTeX parsing WordPress plugin

Adapting from Titus Barik’s “LaTeX Equations and Graphics in PHP” titled article from the Linux Journal magazine, I was able to write a plugin for WordPress that enables me to include LaTeX-type

 $\sum\limits_{j = 1}^m {p\left( X \right)H\left( {Y|X = x_i } \right)} $

in the form of a PNG file format as :

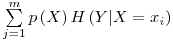
(Although there is problem with multi lined entries such as matrix)

Barik’s article explained the method for Linux, but it can easily be run on a Windows environment (as it is been running on my computer at this very moment). Just install a LaTeX distribution like MikTeX and an image manipulation package like ImageMagick and it’s ready!